Negative Inferences

Author

Marcelo Branco

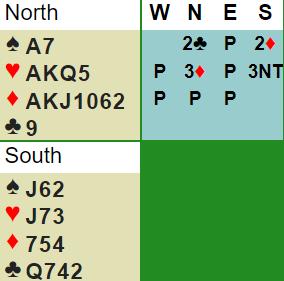
Good declarers are constantly drawing inferences from the cards played by the defenders...

Honor leads usually reveal a touching honor; a high spot indicates that the opening leader is short or lacks high honors in the suit; declarer play is always based on deductions of this sort. 

There are situations which are not as blatant. For example, if you eliminate the side suits in a trump contract and give up the lead so as to force the opponents to break up a suit in which you have Ax in your hand and Q10 in the dummy, if the opponents could choose which hand would win the throw-in trick and LHO won the trick (i.e. he will start the trick and dummy, with Q10, will be the next to play), you may be sure that LHO does not have the King. (If he had the King, he would have let his partner win the trick so as to play the problem suit correctly for the defense). 

There are many discussions, in articles and books, about this theme. But it is not so common to find discussions about what may be called negative inferences, that is, inferences based on what the opponents did not do.

​You are playing in 3NT after a strong 2 Club opening, a 2 Diamond response, a 3 Diamond bid by the strong hand, and 3NT by the weak hand finished the auction. 

The lead was the Five of clubs. East won with the King, and played back the Jack, then the Ten, and finally the Four... and you are still alive since clubs were 4-4 originally. You discarded one spade and 2 diamonds from dummy.

West, upon winning the last club trick, played a spade to dummy's (now) singleton Ace. And now you must guess diamonds to make your contract. You cash the Ace of diamonds (no luck there, all you see are small cards), and play 3 rounds of hearts, ending in hand with your Jack. Everybody follows suit.

Now you play a diamond from your hand, and West plays the 9. What should you do?

If you play the King ("Eight ever, nine never"), you are in effect playing the opening leader to have started with the 3 hearts he has shown, 2 diamonds (only), exactly four clubs, and therefore four spades, i.e., a 4=3=2=4 hand. And if you finesse in diamonds, you are playing for him to have one extra diamond, that can come only at the expense of the spade suit (since the count in the other suits is known by now). That is, you will be playing him for a 3=3=3=4 hand. In the first case, LHO would have had 4 spades and 4 clubs, and he would have led clubs from a suit such as A865. Is that likely? Is it not more probable that he would have led spades (from whichever holding he has in the suit)?

Reasoning like that, I finessed in diamonds, and was rewarded when East showed out.

If you are a math genius, willing to do this kind of calculations in your head while playing the hand (which is not my case, truth be told), you will see that the 4=3=2=4 hand is almost twice as likely as the 3=3=3=4 hand, which is an argument against the diamond finesse. You have to weigh this kind of consideration along with the psychological aspects of the choice of opening lead. As you know by now, in my opinion the psychological clue is dominant in our example hand, but there are situations in which the math is compelling; each player must make his own decisions at the table.